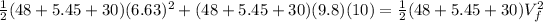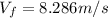Question

Gayle runs at a speed of 4.30 m/s and dives on a sled, initially at rest on the top of a frictionless snow-covered hill. After she has descended a vertical distance of 5.00 m, her brother, who is initially at rest, hops on her back and together they continue down the hill. What is their speed at the bottom of the hill if the total vertical drop is 15.0 m? Gayle's mass is 48.0 kg, the sled has a mass of 5.45 kg and her brother has a mass of 30.0 kg. m/s

Answer 1

`V_f = 8.286 m/s`

Step-by-step explanation:

We will use the energy and the conservation of the linerar mometum for answer this question, so:

First, we will calcule the velocity of the sled when gayle dives in it as:

`P_i = P_f`

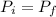
it means that the initial momentum is equal to the finale.

so:

`M_gV_g = M_sV_(si)`

where
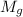`M_g` is the mass of gayle,
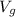`V_g` is the velocity of gayle,
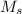`M_s` is the mass of the sled and gayle and
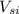`V_(si)` is the velocity of the sled after gayle dives in it

`(48 kg)(4.3 m/s) = (48 kg+5.45 kg)V_(si)`

`V_(si) = 3.86 m/s`

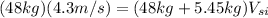
Now, using the conservation of energy, we will calculated what is the velocity of the sled just before the brother of gayle hops on her back. That is:

`M_sgh+(1)/(2)M_sV_(si)^2 = (1)/(2)M_sV_(sf)^2`

where g is the gravity,
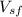`V_(sf)` is the velocity of the sled just before the brother of gayle hops in her back and h is the altitude descended.

`(48 + 5.45)(9.8)(5)+(1)/(2)(48+5.45)(3.86)^2 = (1)/(2)(48 + 5.45)V_(sf)^2`

`V_(sf) = 10.36 m/s`

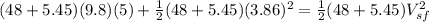
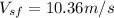
Now, we will know the velocity of the sled after the brother of gayle hops on her back using the conservation of the linear momentum as:

`M_sV_(sf) = M_bV_b`

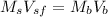
where
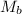`M_b` is the mass of the sled, gayle and now her brother and
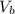`V_b` is the velocity of the sled after the brother of gayle hops on her back.

`(48+5.45)(10.36) = (48+5.45+30)V_b`

`V_b = 6.63 m/s`

Finally using the consevation of energy we will find the velocity at the bottom of the hill as:

`(1)/(2)M_bV_b^2+M_bgh = (1)/(2)M_bV_f^2`

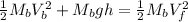
where h = 10 m and
`V_f` is the final velocity, so:

`(1)/(2)(48+5.45+30)(6.63)^2+(48+5.45+30)(9.8)(10) = (1)/(2)(48+5.45+30)V_f^2`

`V_f = 8.286 m/s`