Answer:
(a). The current in the wire is 20.16 A.
(b). The current density is 9.66 A/mm².
Step-by-step explanation:
Given that,
Diameter = 1.63 mm
Drift velocity
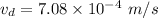
Atomic mass of copper
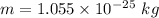
Atomic weight of copper =63.5 g
Density = 9 g/cm³
We need to calculate the number density of electron
Using formula of number density
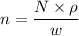
Where, w= atomic weight
Put the value into the formula
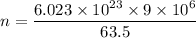
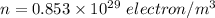
(a).We need to calculate the current in the wire
Using formula of drift velocity
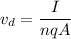
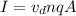
Where, A = cross section area
q = charge of electron
n = number density of electron
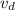 = drift velocity
= drift velocity
Put the value into the formula

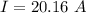
(b). We need to calculate the current density
Using formula of current density

Put the value into the formula
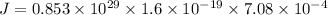
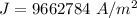
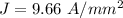
Hence, (a). The current in the wire is 20.16 A.
(b). The current density is 9.66 A/mm².