Answer:
The enthalpy change during the reaction is -7020.09 kJ/mole.
Step-by-step explanation:
First we have to calculate the heat gained by the calorimeter.

where,
q = heat gained = ?
c = specific heat =
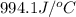
 = final temperature =
= final temperature =
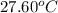
 = initial temperature =
= initial temperature =
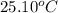
Now put all the given values in the above formula, we get:
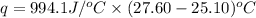
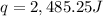
The heat gained by water present in calorimeter. = q'
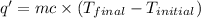
where,
q' = heat gained = ?
m = mass of water =
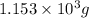
c' = specific heat of water =
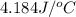
 = final temperature =
= final temperature =
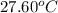
 = initial temperature =
= initial temperature =
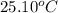

q ' = 12,060.38 J
Now we have to calculate the enthalpy change during the reaction.
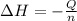
where,
 = enthalpy change = ?
= enthalpy change = ?
Q = heat gained = -(q+q') = -(2,485.25 J + 12,060.38 J)= -14,545.63 J
Q = -14.54563 kJ
n = number of moles fructose =
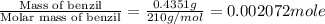
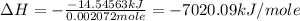
Therefore, the enthalpy change during the reaction is -7020.09 kJ/mole.