Question

To what tension must you adjust the string so that, when vibrating in its second overtone, it produces sound of wavelength 0.767 m ? (Assume that the breaking stress of the wire is very large and isn’t exceeded.)

Answer 1

Tension, T = 547.58 N

Step-by-step explanation:

It can be assumed that,

Mass of the string, m = 8.75 g

Length of the string, l = 70 cm = 0.7 m

Wavelength of produced sound,
`\lambda=0.767\ m`

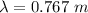
Speed of sound, v = 344 m/s

We know that second overtone is the third harmonic. The frequency in second overtone is given by :

`f=(v)/(3\lambda)`

`f=(344)/(3* 0.767)`

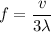
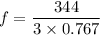
f = 149.5 Hz

The frequency in terms of length is given by :

`f=(1)/(2l)\sqrt{(T)/(m/l)}`

`T=4f^2l^2(m)/(l)`

`T=4f^2lm`

`T=4* (149.5)^2* 0.7* 8.75* 10^(-3)`

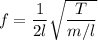
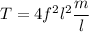
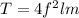
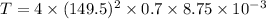
T = 547.58 N

So, the tension in the string is 547.58 N. Hence, this is the required solution.