Question

30 points 1 question PLEASE HELP ME OUT I REALLY NEED IT

Given p(x)=3x^5+2x^2−5, Alonso wants to find out whether 3x+5 is a factor. Which value of x should he evaluate for p(x) to determine the answer?
I got -5/3 which is correct I just need value of the function at the x-value you selected?

Answer 1

p(-5/3) ≠ 0 So, (3 x +5) is NOT A FACTOR of p(x)

Explanation:

Here, the given function is
`p(x)=3x^5+2x^2 - 5`

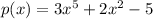
Now, the given root of the function is ( 3x +5)

Now, if ( 3 x + 5) = 0,

we get x = - 5/3

So, the zero of the given polynomial is x = -5/3

Then, x = -5/3, p(x) =0 ⇒ ( 3 x + 5) is a FACTOR of p(x)

Now, let us find the value of function at x = -5/3

Substitute x = -5/3 in the given function p(x), we get:

`p(x)=3x^5+2x^2 - 5  \implies p((-5)/(3))  = 3((-5)/(3))^5 + 2((-5)/(3))^2 - 5\\= 3((-3,125)/(243)) + 2((25)/(9))  - 5\\= ((-3,125)/(81)) + ((50)/(9))  - 5\\= -38.580 + 5.56  - 5  =  -38.02\\\implies p((-5)/(3))  = -38.02`

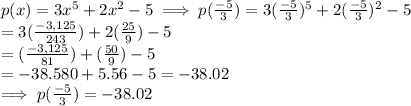
Now, as p(-5/3) ≠ 0 So, (3x +5) is NOT A FACTOR of p(x)