Question

What is the value of a² + 3b = c - 2d when a = 3,6 = 8,0 = 2, d = 5?

Answer 1

What is the value of a^2 + 3b ÷ c - 2d when a = 3, b = 8, c = 2, and d = 5

a. 8

b. 12

c. 10

d. 11

Answer:

Option D

The value of a^2 + 3b ÷ c - 2d when a = 3, b = 8, c = 2, and d = 5 is 11

Solution:

Given that expression is a^2 + 3b ÷ c - 2d

We can use BODMAS rule to solve this expression

BODMAS means brackets, order, division, multiplication, addition and subtraction

According to Bodmas rule, if an expression contains brackets ((), {}, []) we have to first solve or simplify the bracket followed by of (powers and roots etc.), then division, multiplication, addition and subtraction from left to right.

Substitute a = 3, b = 8, c = 2, and d = 5

`a^2 + 3b / c - 2d = 3^2 + 3(8) / 2 -10`

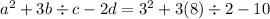
Let us first solve the terms in brackets as per BODMAS rule

`9 + 24 / 2 -10`

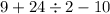
Now perform division as per BODMAS

`9 + 12 -10`

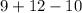
Now peform addition operation

`21 - 10`

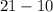
Now peform subtraction operation

21 -10 = 11

Thus the value of a^2 + 3b ÷ c - 2d when a = 3, b = 8, c = 2, and d = 5 is 11