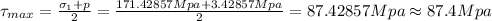Question

The spherical pressure vessel has an inner diameter of 2 m and a thickness of 10 mm. A strain gage having a length of 20 mm is attached to it, and it is observed to increase in length by 0.012 mm when the vessel is pressurized. Determine the pressure causing this deformation, and find the maximum in-plane shear stress, and the absolute maximum shear stress at a point on the outer surface of the vessel. The material is steel, for which Est = 200 GPa and vst = 0.3.

Answer 1

Pressure causing this deformation is 3.43 Mpa

Maximum in-plane shear stress is 0 Mpa

Absolute maximum shear stress at a point on the outer surface of the vessel is 87.4 Mpa

Step-by-step explanation:

Maximum normal strain is
`\frac {0.012}{20}=0.0006`

`\frac {pr (1-v)}{2Et}=0.0006`

`\frac {p* 1000mm(1-0.3)}{2* 200* 10^(3)* 10}`

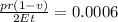
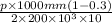
P=3.42857 Mpa

Therefore, internal pressure causing deformation is
`3.42857 Mpa\approx 3.43 Mpa`

Stress along direction 1 and 2 is given by
`\frac {pr}{2t}`

`\sigma_1=\sigma_2=\frac {pr}{2t}=\frac {3.42857* 1000mm}{2* 10 mm}=171.42857 Mpa`

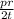
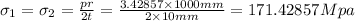
Maximum in-plane shear stress is given by
`\frac {\sigma_1-\sigma_2}{2}=\frac {171.42857 Mpa-171.42857 Mpa}{2}=0 Mpa`

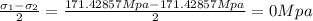
Absolute maximum shear stress,
`\tau_(max)=\frac {\sigma_1+p}{2}=\frac {171.42857 Mpa+3.42857 Mpa}{2}=87.42857 Mpa\approx 87.4 Mpa`