Question

Rebecca is a real estate agent who would like to find evidence supporting the claim that the population mean market value of houses in the neighborhood where she works is greater than $250,000. To test the claim, she randomly selects 35 houses in the neighborhood and finds that the sample mean market value is $259,860 with a sample standard deviation of $24.922. The test statistic t for a hypothesis test of H0 : μ = 250.000 versus Ha : μ > 250.000 is t 2.34 , which has 34 degrees of freedom. If 0.01

Answer 1

Option C) There are enough evidence that at significance level of 0.05 to support the claim that the the population mean market value of houses in the neighborhood where she works is greater than $250,000.

Explanation:

We are given the following in the question:

Population mean, μ = $250,000

Sample mean,
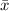`\bar{x}` = $259,860

Sample size, n = 35

Alpha, α = 0.05

Sample standard deviation, σ = $24.922

First, we design the null and the alternate hypothesis

`H_(0): \mu = 250,000\text{ dollars}\\H_A: \mu > 250,000\text{ dollars}`

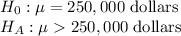
We use One-tailed t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) } = 2.34`

`0.01 < \text{ p-value }< 0.025`

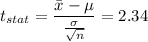
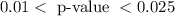
Since the p-value is less than the significance level, we fail to accept the null hypothesis.

There are enough evidence that at significance level of 0.05 to support the claim that the the population mean market value of houses in the neighborhood where she works is greater than $250,000.