Question

Katie Pairy Fruits Inc. has a $1,700 18-year bond outstanding with a nominal yield of 18 percent (coupon equals 18% × $1,700 = $306 per year). Assume that the current market required interest rate on similar bonds is now only 12 percent. Use Appendix B and Appendix D for an approximate answer but calculate your final answer using the formula and financial calculator methods. a. Compute the current price of the bond. (Do not round intermediate calculations. Round your final answer to 2 decimal places. Assume interest payments are annual.) b. Find the present value of 6 percent × $1,700 (or $102) for 18 years at 12 percent. The $102 is assumed to be an annual payment. Add this value to $1,700. (Do not round intermediate calculations. Round your final answer to 2 decimal places. Assume interest payments are annual.) Present value $ ReferenceseBook & Resources WorksheetDifficult.

Answer 1

a) The present value of the bond is $2,439.47

b) If the coupon of the bond changes to 6%, the present value of the bond would be $960.53

Step-by-step explanation:

Hi, in order to answer the questions, we need to use the following formula.

`Price=(Coupon((1+Yield)^(n)-1) )/(Yield(1+Yield)^(n) ) +(FaceValue)/((1+Yield)^(n) )`

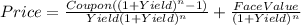
Where:

Coupon = 0.18*$1,700= $306

Yield = Discount rate (in our case, 12% or 0.12)

n = years to maturity (in our case, 18)

Face Value = $1,700

So, to find the price of the bond today, everything should look like this:

`Price=(306((1+0.12)^(18)-1) )/(0.12(1+0.12)^(18) ) +(1,700)/((1+0.12)^(18) )`

`Price= 2,218.40 +221.07=2,439.47`

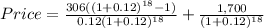
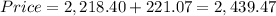
Therefore, the price is $2,439.47

Using the same equation, the answer to b) is

`Price=(102((1+0.12)^(18)-1) )/(0.12(1+0.12)^(18) ) +(1,700)/((1+0.12)^(18) )`

`Price= 960.53`

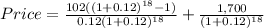
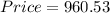
The answer to b) is $960.53

Best of luck.