Question

A simple pendulum consists of a point mass suspended by a weightless, rigid wire in a uniform gravitation field. Which of the following statements are true when the system undergoes small oscillations? Check all that apply. a. The period is independent of the length of the wire. b. The period is inversely proportional to the length of the wire. c. The period is independent of the suspended mass. d. The period is proportional to the suspended mass. e. The period is proportional to the square root of the length of the wire. f. The period is inversely proportional to the suspended mass.

Answer 1

Option (c) and (e)

Step-by-step explanation:

In case of a simple pendulum having suspended mass 'M', if the length of the wire is 'L', and the acceleration due to gravity that acts on it is 'g', then the time period, 'T' of the pendulum for one complete oscillation is given by:

`T = 2\pi \sqrt{(L)/(g)}`

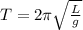
From the above equation, we can say that:

• Time period of the pendulum does not depend on the suspended mass.
• Time period is in direct proportion to the square root of the wire length
• Time period is depends inversely on the acceleration due to gravity.