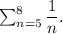Answer: The given sums in sigma notation are
(a)
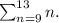
(b)
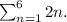
(c)
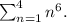
(d)
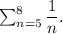
Step-by-step explanation: We are given to express the following sums using sigma notation.
(a) 9 plus 10 plus 11 plus 12 plus 13.
Here, sum is
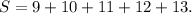
In sigma notation, the given sum can be written as follows :
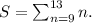
(b) 2 plus 4 plus 6 plus 8 plus 10 plus 12.
Here, sum is
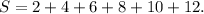
In sigma notation, the given sum can be written as follows :
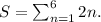
(c) 1 Superscript 6 Baseline plus 2 Superscript 6 Baseline plus 3 Superscript 6 Baseline plus 4 Superscript 6.
Here, sum is
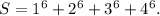
In sigma notation, the given sum can be written as follows :
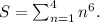
(d) one fifth plus one sixth plus one seventh plus one eighth.
Here, sum is
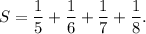
In sigma notation, the given sum can be written as follows :
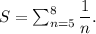
Thus, the given sums in sigma notation are
(a)
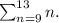
(b)
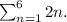
(c)
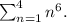
(d)