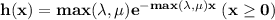Question

The lifetime of two light bulbs are modeled as independent and exponential random variables X and Y, with parameters lambda and mu, respectively. The time at which one of those two light bulb first burns out is Z = min (X, Y), what is the PDF of Z?

Answer 1

`\bf h(x)=max(\lambda,\mu) e^(-max(\lambda,\mu) x)\;(x\geq0)`

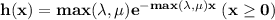
Explanation:

The PDF of X is

`\bf f(x)=\lambda e^(-\lambda x)\;(x\geq0)`

The PDF of Y is

`\bf g(x)=\mu e^(-\mu x)\;(x\geq0)`

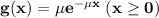
The means of X and Y are respectively,

`\bf \displaystyle(1)/(\lambda)\;,\displaystyle(1)/(\mu)`

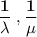
so we can see that the larger the parameter, the smaller the mean. Hence the PDF of Z = min(X, Y) is an exponential with the largest parameter of the two.

Therefore, the PDF of Z is

`\bf h(x)=max(\lambda,\mu) e^(-max(\lambda,\mu) x)\;(x\geq0)`