Question:
For f(x) = 3x+1 and g(x) = x^2 - 6, find (f - g)(x)
O A. 3x² - 17
O B. x^2 – 3x-7
O C. -x^2+3x+7
O D. - x^2 + 3x - 5
Answer:
Option C
For f(x) = 3x+1 and g(x) = x^2 - 6 then the value of
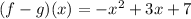
Solution:
Given that,
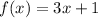
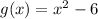
To find: (f - g)(x)
We know that,
(f – g)(x) = f (x) – g(x)
Let us substitute the given values of f(x) and g(x) to find (f – g)(x)
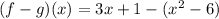
On multiplying the negative sign with terms inside second bracket
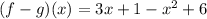
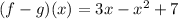
On rearranging the terms we get,
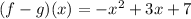
Thus the value of (f - g)(x) is found out and option C is correct