Question

For f(x) = 3x+1 and g(x) = x2 - 6, find (f - g)(x).

O A. 3x² - 17
O B. x2 – 3x-7
O C. -x2+3x+7
O D. - x2 + 3x - 5

Answer 1

Question:

For f(x) = 3x+1 and g(x) = x^2 - 6, find (f - g)(x)

O A. 3x² - 17

O B. x^2 – 3x-7

O C. -x^2+3x+7

O D. - x^2 + 3x - 5

Answer:

Option C

For f(x) = 3x+1 and g(x) = x^2 - 6 then the value of
`(f - g)(x) = - x^2 + 3x + 7`

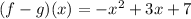
Solution:

Given that,

`f(x) = 3x + 1`

`g(x) = x^2 - 6`

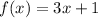
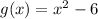
To find: (f - g)(x)

We know that,

(f – g)(x) = f (x) – g(x)

Let us substitute the given values of f(x) and g(x) to find (f – g)(x)

`(f - g)(x) = 3x + 1 - (x^2 - 6)`

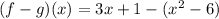
On multiplying the negative sign with terms inside second bracket

`(f - g)(x) = 3x + 1 - x^2 + 6`

`(f - g)(x) = 3x - x^2 + 7`

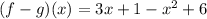
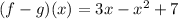
On rearranging the terms we get,

`(f - g)(x) = - x^2 + 3x + 7`

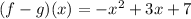
Thus the value of (f - g)(x) is found out and option C is correct