Answer:
The length of the diagonal is closest to 51 cm.
Explanation:
Given:
TV screen is 41 cm long and 31 cm high.
Now, to find the length of the diagonal.
By using pythagorean theorem:
leg 1 = 41 cm, leg 2 = 31 cm.
Let the hypotenuse be
 .
.
(leg 1)² + (leg 2)² = hypotenuse²
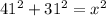
⇒
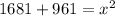
⇒
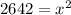
Using square root on both sides we get:
⇒
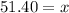
So, the length of the diagonal = 51.40 cm.
By rounding off of 51.40cm it becomes 51 cm.
Therefore, the length of the diagonal is closest to 51 cm.