Question

The altitude (i.e., height) of a triangle is increasing at a rate of 1.5 cm/minute while the area of the triangle is increasing at a rate of 4.5 square cm/minute. At what rate is the base of the triangle changing when the altitude is 7.5 centimeters and the area is 80 square centimeters?

Answer 1

Rate at which base is decreasing is 3.07 cm /min

Step-by-step explanation:

We have area of triangle,

A = 0.5 bh

Where b is base and h is altitude.

Differentiating with respect to time

`A=0.5bh\\\\(dA)/(dt)=0.5* \left ( b* (dh)/(dt)+h* (db)/(dt)\right )`

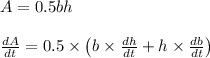
Here area is 80 square centimeters and altitude is 7.5 centimeters,

So we have

A = 0.5 bh

80 = 0.5 x b x 7.5

b = 21.33 cm

We also have

`(dh)/(dt)=1.5cm/min\\\\(dA)/(dt)=4.5cm^2/min`

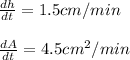
Substituting in differentiated equation

`(dA)/(dt)=0.5* \left ( b* (dh)/(dt)+h* (db)/(dt)\right )\\\\4.5=0.5* \left ( 21.33* 1.5+7.5* (db)/(dt)\right )\\\\9= 32+7.5* (db)/(dt)\\\\(db)/(dt)=-3.07cm/min`

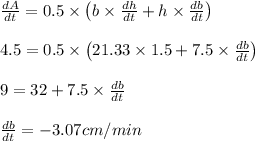
Rate at which base is decreasing = 3.07 cm /min