Question

The length of a rectangle is 5 inches less than twice it’s width. If the rectangle has a perimeter of 80 inches, find the length and the width.

Answer 1

Length = 25 Inches,

Breadth = 15 Inches

Explanation:

Let the length of the rectangle be X inches and breadth of the rectangle be Y Inches .

So, according to question,

X = 2Y - 5.

Now, Perimeter of rectangle will be 2(X + Y) Inches,

Which is given to be 80 Inches.

Thus, X + Y = 40

2Y - 5 + Y = 40

3Y = 45

Y = 15 Inches

X = 2(15) - 5 = 25

= 25 Inches.

So, Length = 25 Inches,

Breadth = 15 Inches

Answer 2

Length of a rectangle is 25 inches.

Width of a rectangle is 15 inches.

Explanation:

Given:

Let length of a rectangle be given by ' L'

and Width of rectangle be given by x inches.

According to the given condition,

Length = L = 2x -5

Width = x

Perimeter of a rectangle = 80 inches

To Find:

Length = ?

Width = ?

Solution:

We know Perimeter of a rectangle given by formula,

`\textrm{Perimeter of a rectangle }=2( Length + Width)`

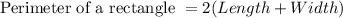
substituting the given values in the above equation we get

`\textrm{Perimeter of a rectangle }=2( (2x-5)+x)\\\textrm{applying distributive property we get }\\80=( 4x-10+2x)\\6x=80+10\\6x=90\\x=(90)/(6) \\x=15\ inches\\`

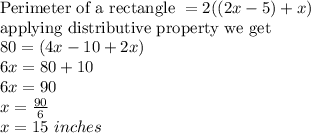
∴ Length = 2x - 5

= 2×15 - 5

= 30 - 5

= 25 inches

∴ Length = (2x - 5) = 25 inches

∴ Width = x = 15 inches

Length of a rectangle is 25 inches.

Width of a rectangle is 15 inches.