Question

A metal rod with a length of 22.0cm lies in the xy-plane and makes an angle of 37.9 degrees with the positive x-axis and an angle of 52.1degrees with the positive y-axis. The rod is moving in the +x-direction with a speed of 6.80m/s . The rod is in a uniform magnetic field B =(0.170T)i^-(0.240T)j^-(0.0900T )k^.

What is the magnitude of the emf induced in the rod?

Answer 1

Induced emf in the rod is,
`\epsilon=0.08262\ V`

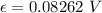
Step-by-step explanation:

Given that,

Length of the rod, L = 22 cm = 0.22 m

Angle with x axis is 37.9 degrees with the positive x-axis and an angle of 52.1 degrees with the positive y-axis.

`L=0.22(cos37.9\ i)+0.22(sin37.9\ j)`

`L=(0.173\ i+0.135\ j)\ m`

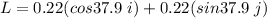
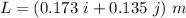
Velocity of the rod, v = 6.8i m/s

Magnetic field,
`B=0.170i-0.24j-0.09k`

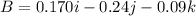
The formula for the emf induced in the rod is given by :

`\epsilon=(v* B){\cdot}L`

`\epsilon=(6.8i* (0.170i-0.24j-0.09k)){\cdot} (0.173\ i+0.135\ j)`

`\epsilon=(0.612j-1.632k){\cdot}(0.173i+0.135j)`

`\epsilon=0.08262\ V`

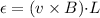
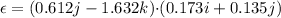
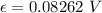
So, the magnitude of the emf induced in the rod is 0.08262 volts. Hence, this is the required solution.