Question

A coil of area 0.2 m2 and total resistance 100 Ω is rotated at a rate of 60 rev/s. Its axis of rotation is perpendicular to a 0.5 T magnetic field. How many turns are in the coil if energy is delivered to it at a maximum rate of 1420 W?

Answer 1

The concept necessary to solve this problem is the mathematical definition of the electromotive force or induced voltage. Theoretically the electromotive force is the electrical action produced by a non-electrical source. Mathematically it can be expressed as

`\epsilon = NBA\omega`

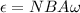
Where

N = Number of loops

B = Magnetic Field

A = Cross-sectional Area

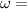`\omega =` Angular velocity

Re-arrange to find N,

`N = (\epsilon)/(BA\omega)`

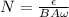
In parallel, we can also consider the rate of energy change expressed in terms of the induced voltage, that is,

`P = (\epsilon^2)/(R)`

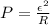
Where

R = Resistance

The previous equation can be expressed as

`\epsilon=√(PR)`

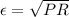
Equating the two expression we have

`N = (√(PR))/(BA\omega)`

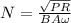
Replacing with our values we have that

`N = (√((1420)(100)))/((0.5)(0.2)(60*2\pi))`

`N=9.9957 \approx 10`

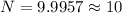
Therefore the number of turns are 10.