Question

drag and drop the constant of proportionality into the box to match the table. if the table is not proportional drag and drop not proportional, drag and drop not proportional into the box

Answer 1

1. Not proportional.

2. k = 0.5

3.
`k = (2)/(3)`

4.
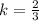
`k = (3)/(4)`

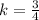
Explanation:

The constant for any proportionality relation is given by
`k = (y)/(x)`.

Therefore, for the pair of values (2,0), k = 0, hence, the relation is not proportional.

Now, for the peir of values (4,2),
`k = (2)/(4) = 0.5`.

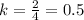Now, for the pair of values of x and y, (6,4), the value of
`k = (4)/(6) = (2)/(3)`

Finally, for the pair of values of x and y, (8,6), the value of
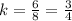`k = (6)/(8) = (3)/(4)` (Answer)

Answer 2

The given table is not proportional.

Explanation:

If a table represents a proportional relationship then

`y\propto x`

`y=kx`

where, k is constant of proportionality.

`(y)/(x)=k`

It means the ratio of y and x remains same.

For given table,

`(y_1)/(x_1)=(0)/(2)=0`

`(y_2)/(x_2)=(2)/(4)=0.5`

`(y_1)/(x_1)\\eq (y_2)/(x_2)`

Therefore, the given table is not proportional.