Answer:
47.83W
Step-by-step explanation:
Suppose that Δm of water is pumped in time Δt
The potential energy of the water increases by the steady pumping of water.
ΔU = (Δm)gh
where,
h is the vertical distance through which it is lifted, and
This increases the kinetic energy by
ΔK =
 (Δm)v²
(Δm)v²
where v is its final speed
The workdone is given by;
ΔW = ΔU + ΔK
⇒ ΔW = (Δm)gh +
 (Δm)v²
(Δm)v²
and its power is given by;
P = ΔW/Δt
⇒ P = Δm/Δt (gh +
 (Δm)v²)
(Δm)v²)
The rate of mass flow is Δm/Δt = ρ × A × v
∴ Rate of mass flow = ρAv
where,
ρ is the density of water
A is the area of the hose
A = πr²
A = π (0.0089)² = 2.49 × 10⁻⁴ m²
Rate of mass flow ρAv = (1000kg/m³) x (2.49 × 10⁻⁴ m²) x (6.1 m/s)
= 1.52 kg/s
The power of the pump is;
P = ρAv (gh +
 (Δm)v²)
(Δm)v²)
P = (1.52kg/s)( (9.8m/s² × 2.9m) +
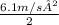 1)
1)
P = 1.52 × 31.47
P = 47. 83W