Answer:
7270.7 Pa
Step-by-step explanation:
g = Acceleration due to gravity = 9.8 m/s²
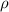 = Density of liquid = 1025 kg/m³
= Density of liquid = 1025 kg/m³
h = Height = 90 cm
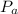 = Pressure =
= Pressure =
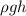
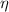 = Viscosity = 0.001 Pas
= Viscosity = 0.001 Pas
l = Length of needle = 2 cm
r = Radius of needle = 0.2 mm
P = Absolute pressure
Q = Flow rate =
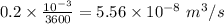
From Poiseuille's equation we have
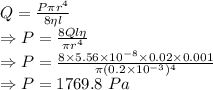
This pressure is the absolute pressure
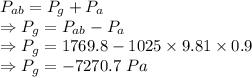
The average gauge pressure inside the vein where the needle is is 7270.7 Pa (ignoring the negative sign)