Answer:
a)
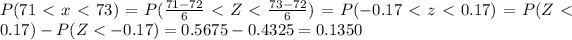
b)
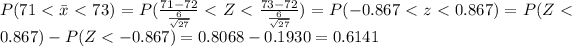
c) Is the probability in part (b) much higher? YES very high compared with part a
The probability in part (b) is much higher because the standard deviation is smaller for the x distribution.
iii. The probability in part (b) is much lower because the standard deviation is smaller for the x distribution.
Explanation:
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
Let X the random variable that represent variable in the population, and for this case we know the distribution for X is given by:
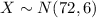
Where
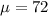 and
and
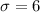
And let
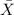 represent the sample mean, the distribution for the sample mean is given by:
represent the sample mean, the distribution for the sample mean is given by:

On this case
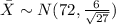
Part a
(a) What is the probability that an 18-year-old man selected at random is between 71 and 73 inches tall? (Round your answer to four decimal places.)
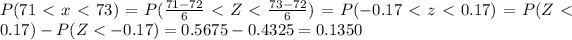
(b) If a random sample of twenty-seven 18-year-old men is selected, what is the probability that the mean height x is between 71 and 73 inches? (Round your answer to four decimal places.)

c) Compare your answers to parts (a) and (b). Is the probability in part (b) much higher?
Is the probability in part (b) much higher? YES very high compared with part a
The probability in part (b) is much higher because the standard deviation is smaller for the x distribution.
iii. The probability in part (b) is much lower because the standard deviation is smaller for the x distribution.