Question

Question 6 2 pts

In an agricultural study, the average amount of corn yield is normally distributed with a mean of 189.3 bushels of corn per acre, with a standard deviation of 23.5 bushels of corn. If a study included 1200 acres, about how many would be expected to yield more than 180 bushels of corn per acre?

346 acres
654 acres
785 acres
415 acres

Answer 1

785 acres

Explanation:

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

Let X represent the random variable amount of corn yield

Assuming the X follows a normal distribution

`X \sim N(\mu, \sigma)`

And we know that the average
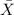`\bar X` is dsitributed:

`\bar X \sim N(\mu=189.3, \sigma_(\bar X)=23.5)`

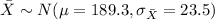
And we are interested on this probability:

`P(\bar X>180)`

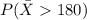
For this case we can use the z score formula given by:

`z=(\bar X -\mu)/(\sigma_(\bar X))`

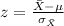
If we apply this we got:

`P(\bar X>180)=P(Z>(180-189.3)/(23.5))=P(Z>-0.396)=1-P(Z<-0.396)=1-0.346=0.654`

And since we have a proportion estimated and we hava a total of 1200 acres the expected to yield more than 180 bushels of corn per acre would be:

`r=1200*0.654=784.8`

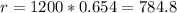
And if we round up this amount we got
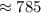`\approx 785` and that would be the best option for this case.