Answer:
0.0015 is he probability that a randomly selected student has a body weight of greater than 169 pounds.
Explanation:
We are given the following information in the question:
Mean, μ = 142 pounds
Standard Deviation, σ = 9 pounds
We are given that the distribution of body weights is a bell shaped distribution that is a normal distribution.
Empirical Rule:
- The empirical rule states that for a normal distribution 68% falls within the first standard deviation from the mean, 95% within the first two standard deviations from the mean and 99.7% within three standard deviations of the mean.
P( body weight of greater than 169 pounds)
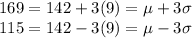
According to empirical rule, 99.7% within three standard deviations of the mean.
Thus, we can write:
P( body weight of greater than 169 pounds)
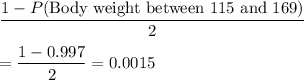
0.0015 is he probability that a randomly selected student has a body weight of greater than 169 pounds.