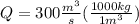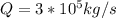Question

Water is flowing in a drainage channel of rectangular cross-section. The width of the channel is 15 m, the depth of water is 8.0 m, and the speed of the flow is 2.5 m/s. What is the flow rate in kg/s?

2.0 · 105 kg/s
2.0 · 103 kg/s
3.0 · 105 kg/s
3.0 · 103 kg/s
3.0 · 102 kg/s

Answer 1

To solve this problem we will use the concepts related to the flow rate, which describes the volumetric amount of a fluid that travels a point in a given time. Mathematically it can be expressed as

Q = AV

Where

A= Area

V = Volume

Our values are given as

`A = 15*8 = 120m^2`

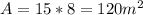
V = 2.5m/s

Replacing we have to

`Q = 120*2.5`

`Q = 300m^3/s`

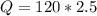
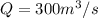
At this point we know that 1 m ^ 3 of water is equivalent to 1000Kg (Its value in density at normal conditions)

`Q = 300(m^3)/(s) ((1000kg)/(1m^3))`

`Q= 3*10^5kg/s`