Question

Set up a Hess’s law cycle, and use the following information to calculate ΔH∘f for aqueous nitric acid, HNO3(aq). You will need to use fractional coefficients for some equations.

3NO2(g)+H2O(l)→ 2HNO3(aq)+NO(g) ΔH∘ = -137.3 kJ
2NO(g)+O2(g)→ 2NO2(g) ΔH∘ = -116.2 kJ
4NH3(g)+5O2(g)→ 4NO(g)+6H2O(l) ΔH∘ = -1165.2 kJ
NH3(g) ΔH∘f = -46.1 kJ
H2O(l) ΔH∘f = -285.8 kJ

Answer 1

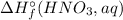`\Delta H_(f)^(\circ ) (HNO_(3), aq)` = (-207.39) kJ/mol

Step-by-step explanation:

Given:

`\Delta H_(f)^(\circ ) (NH_(3), g)= -46.1 kJ/mol\\ \Delta H_(f)^(\circ ) (H_(2)O, l)= -285.8 kJ/mol\\ \Delta H_(f)^(\circ ) (HNO_(3), aq)= ? kJ/mol`

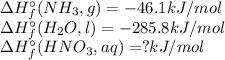
3NO₂(g)+H₂O(l)→ 2HNO₃(aq)+NO(g); ΔH° = -137.3 kJ ....equation 1

2NO(g)+O₂(g)→ 2NO₂(g) ; ΔH° = -116.2 kJ ....equation 2

4NH₃(g)+5O₂(g)→ 4NO(g)+6H₂O(l) ;ΔH° = -1165.2 kJ ....equation 3

Multiplying equation 1 with (2/3), we get

2NO₂(g) + 2/3 H₂O(l) → 4/3 HNO₃(aq) + (2/3) NO(g) ....equation 4

Adding equation 2 and 4, we get

2NO₂(g) + 2/3 H₂O(l) + 2NO(g) + O₂(g) → 4/3 HNO₃(aq) + (2/3) NO(g) + 2NO₂(g)

⇒ (4/3) NO(g) + O₂(g) + 2/3 H₂O(l) → 4/3 HNO₃(aq) ....equation 5

Multiplying equation 3 with (1/3), we get

(4/3) NH₃(g) + (5/3) O₂(g) → (4/3) NO(g)+ 2 H₂O(l) ....equation 6

Now adding equation 5 and 6, we get

(4/3) NH₃(g) + (5/3) O₂(g) + (4/3) NO(g) + O₂(g) + 2/3 H₂O(l) → (4/3) NO(g)+ 2 H₂O(l) + 4/3 HNO₃(aq)

⇒ (4/3) NH₃(g) + (8/3) O₂(g) → (4/3) HNO₃(aq) + (4/3) H₂O(l) ....equation 7

Now multiplying equation 7 with (3/4), we get

NH₃(g) + 2 O₂(g) → HNO₃(aq) + H₂O(l) ...equation 8

Therefore, by Hess's law the standard enthalpy of formation is:

ΔH° = (3/4) [ (-137.3 kJ) × (2/3) + (-116.2 kJ) + (-1165.2 kJ) × (1/3)]

ΔH° = (3/4) [ - 91.53 - 116.2 - 388.4]

ΔH° = (3/4) [-596.13] = -447.09 kJ

Since the change in enthalpy of a reaction:

ΔH° =
`[\Delta H_(f)^(\circ ) (HNO_(3), aq) + \Delta H_(f)^(\circ ) (H_(2)O, l)] - [\Delta H_(f)^(\circ ) (NH_(3), g) + 2 \Delta H_(f)^(\circ ) (O_(2), g)]`

(-447.09 kJ) =
`[\Delta H_(f)^(\circ ) (HNO_(3), aq)` + (-285.8 kJ)] - [-46.1 kJ + 2 (0 kJ)]

⇒
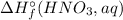`\Delta H_(f)^(\circ ) (HNO_(3), aq)` = (-447.09) + 285.8 kJ - 46.1 kJ

⇒
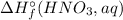`\Delta H_(f)^(\circ ) (HNO_(3), aq)` = (-207.39) kJ/mol