Question

16.34 g of CuSO4 dissolved in water giving out 55.51 kJ and 25.17 g CuSO4•5H2O absorbs 95.31 kJ. From the following reaction cycle and the experimental data above, calculate the enthalpy of hydration of CuSO4.

Answer 1

The enthalpy of hydration of copper sulphate is -1486.62 kJ/mol which means 1486.62kJ of energy is absorbed by one mole of copper sulphate during the process of hydration

Step-by-step explanation:

Step 1: Determine the energy released per mole of
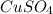`CuSO_(4)` dissolved

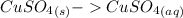`{CuSO_(4)}_((s)) -> {CuSO_(4)}_((aq))` (Eq. 1)

`n_{CuSO_(4)} = \frac{m_{CuSO_(4)}}{M_{CuSO_(4)}}`

`n_{CuSO_(4)} = (16.34)/(159.5)`

`n_{CuSO_(4)} = 0.102 mol`

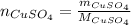
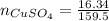
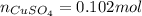
If 0.102 moles of
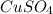`CuSO_(4)` releases 55.51kJ of energy, 1 mole will release 541.85kJ/mol

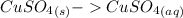`{CuSO_(4)}_((s)) -> {CuSO_(4)}_((aq))` ΔH = -541.85kJ/mol

Step 2: Determine the energy released per mole of
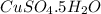`CuSO_(4).5H_(2)O` dissolved

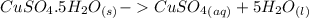`{CuSO_(4).5H_(2)O}_((s)) -> {CuSO_(4)}_((aq))+{5H_(2)O}_((l))` (Eq. 2)

`n_{CuSO_(4).5H_(2)O} = \frac{m_{CuSO_(4).5H_(2)O}}{M_{CuSO_(4).5H_(2)O}}`

`n_{CuSO_(4).5H_(2)O} = (25.17)/(249.5)`

`n_{CuSO_(4).5H_(2)O} = 0.101 mol`

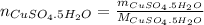
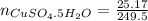
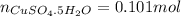
If 0.101 moles of
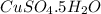`CuSO_(4).5H_(2)O` absorbs 95.31kJ of energy, 1 mole will absorb 944.77kJ/mol

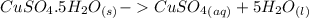`{CuSO_(4).5H_(2)O}_((s)) -> {CuSO_(4)}_((aq))+{5H_(2)O}_((l))` ΔH = 944.77kJ/mol

Step 3: Subtracting Eq. 2 from Eq. 1

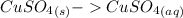`{CuSO_(4)}_((s)) -> {CuSO_(4)}_((aq))` ΔH = -541.85kJ/mol (Eq. 1)

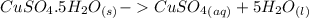`{CuSO_(4).5H_(2)O}_((s)) -> {CuSO_(4)}_((aq))+{5H_(2)O}_((l))` ΔH = 944.77kJ/mol (Eq. 2)

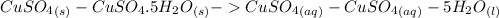`{CuSO_(4)}_((s)) -{CuSO_(4).5H_(2)O}_((s)) -> {CuSO_(4)}_((aq)) -{CuSO_(4)}_((aq))-{5H_(2)O}_((l))` ΔH = -541.85-944.77

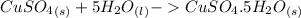`{CuSO_(4)}_((s))+{5H_(2)O}_((l)) -> {CuSO_(4).5H_(2)O}_((s))` ΔH = -1486.62 kJ/mol