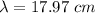Answer:
(a)
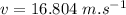
(b)
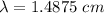
(c)
and
Step-by-step explanation:
Given:
- frequency of vibration,
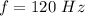
- mass of object attached to the rope,
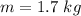
- linear mass density of rope,
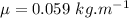
(a)
We have the expression for velocity as:
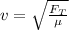 .................(1)
.................(1)
where:
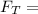 tension force in the rope
tension force in the rope
Now for tension force we balance the forces acting on the rope:
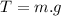
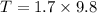
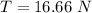
Now using eq. (1)

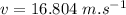
(b)
Wavelength is given by:
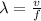

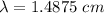
(c)
- On increasing the mass to 2.8 kg
We get :


and