Question

The free-fall acceleration on the surface of Mercury is about three eighths that on the surface of the Earth. The radius of Mercury is about 0.375 RE (RE = Earth's radius = 6.4 106 m). Find the ratio of their average densities, ?Mercury/?Earth.

Answer 1

1

Step-by-step explanation:

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

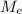`M_e` = Mass of Earth

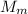`M_m` = Mass of Mercury

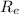`R_e` = Radius of Earth

`R_m` = Radius of Mercury =
`0.375R_e`

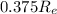
Mass is given by

`M=\rho v\\\Rightarrow M=\rho (4)/(3)\pi R^3`

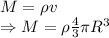
Acceleration due to gravity on Earth

`g_e=(GM_e)/(R_e^2)\\\Rightarrow g_e=(G\rho_e (4)/(3)\pi R_e^3)/(R_e^2)`

Acceleration due to gravity on Mercury

`g_m=(GM_m)/(R_m^2)\\\Rightarrow g_m=(G\rho_e (4)/(3)\pi (0.375R_e)^3)/((0.375R_e)^2)`

According to the question

`(g_m)/(g_e)=(3)/(8)`

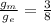
So,

`(3)/(8)=((G\rho_e (4)/(3)\pi (0.375R_e)^3)/((0.375R_e)^2))/((G\rho_e (4)/(3)\pi R_e^3)/(R_e^2))\\\Rightarrow (3)/(8)=(\rho_m0.375)/(\rho_e)\\\Rightarrow (\rho_m)/(\rho_e)=(3)/(8* 0.375)\\\Rightarrow (\rho_m)/(\rho_e)=1`

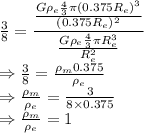
Hence, the average density ratio of Mercury to Earth is 1