The college will receive approximately $36,824.32 after 40 years.
To solve this problem
We can use the formula for continuous compound interest:

Where
- A is the total sum.
- P stands for principle (deposit) initially.
- e is equal to Euler's number, or around 2.71828.
- The interest rate, expressed in decimal form, is r.
- t is the number of years.
In this case, the initial principal (P) is $4,000, the interest rate (r) is 5.5% (or 0.055 as a decimal), and the time (t) is 40 years.
Plugging in the values into the formula, we have:
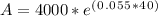
Now, we can evaluate
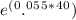 to approximately 2.71828^(2.2) which is roughly 9.206
to approximately 2.71828^(2.2) which is roughly 9.206
So, the final amount (A) that the college will receive is:
A = 4000 * 9.206 = $36,824.32
So, the college will receive approximately $36,824.32 after 40 years.