Answer: 49.85%
Explanation:
Given : The physical plant at the main campus of a large state university recieves daily requests to replace florecent lightbulbs. The distribution of the number of daily requests is bell-shaped ( normal distribution ) and has a mean of 61 and a standard deviation of 9.
i.e.
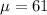 and
and
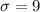
To find : The approximate percentage of lightbulb replacement requests numbering between 34 and 61.
i.e. The approximate percentage of lightbulb replacement requests numbering between 34 and
 .
.
i.e. i.e. The approximate percentage of lightbulb replacement requests numbering between
 and
and
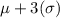 . (1)
. (1)
According to the 68-95-99.7 rule, about 99.7% of the population lies within 3 standard deviations from the mean.
i.e. about 49.85% of the population lies below 3 standard deviations from mean and 49.85% of the population lies above 3 standard deviations from mean.
i.e.,The approximate percentage of lightbulb replacement requests numbering between
 and
and
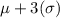 = 49.85%
= 49.85%
⇒ The approximate percentage of lightbulb replacement requests numbering between 34 and 61.= 49.85%