Question

Test the claim that the two samples described below come from populations with the same mean. Assume that the samples are independent simple random samples.Sample 1: n1=24, x?? 1=14, s1=4.Sample 2: n2=28, x?? 2=9, s2=4.(a) The test statistic is ___.(b) Find the t critical value for a significance level of 0.02 for an alternative hypothesis that the first population has a larger mean (one-sided test): t?= ___.(c) The conclusion is-There is not sufficient evidence to warrant rejection of the claim that the two populations have the same mean.-There is sufficient evidence to warrant rejection of the claim that the two populations have the same mean and accept that the first population has a larger mean.

Answer 1

a. t= (X[bar]₁ - X[bar]₂) - (μ₁ - μ₂) ~
`t_(n₁ + n₂-2)`

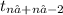
Sa √(1/n₁ + 1/n₂)

b. t_{50; 0.98} = 2.109[/tex]

c. There is sufficient evidence to warrant rejection of the claim that the two populations have the same mean and accept that the first population has a larger mean.

Explanation:

Hello!

You have two random samples and it's believed that both samples have the same population mean. Symbolically: μ₁ = μ₂

a.

The statistic to use, to test the difference of population mean, assuming that both variables have a normal distribution and with unknown but equal population variances, is a pooled t.

t= (X[bar]₁ - X[bar]₂) - (μ₁ - μ₂) ~
`t_(n₁ + n₂-2)`

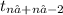
Sa √(1/n₁ + 1/n₂)

b. If the hypothesis is that the mean of the first sample is greater than the mean of the second sample :

H₀: μ₁ = μ₂

H₁: μ₁ > μ₂

α: 0.02

The critical value is:

`t_(n₁ + n₂-2;1-\alpha ) = t_(50; 0.98) = 2.109`

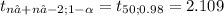
The rejection region is one-tailed. If the calculated value is equal or greater than 2.109, then you reject the null hypothesis. If the value is less than the critical value, then you do not reject the null hypothesis.

c.

t= (X[bar]₁ - X[bar]₂) - (μ₁ - μ₂) = (14-9) - 0 = 4.49

Sa √(1/n₁ + 1/n₂) 4√(1/24 + 1/28)

Since the calculated value is greater than the critical value, then you reject the null hypothesis. In other words, the population mean of the first population is greater than the population mean of the second population.

I hope it helps!