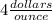Answer:
Part 1) The unit rate is
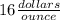
Part 2) The unit rate is

Part 3) The unit rate is

Part 4) The unit rate is
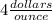
see the attached figure
Explanation:
we know that
The formula to calculate the slope between two points is equal to
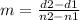
where
d ----> number of dollars (dependent variable or output value)
n ---> number of ounces (independent variable or input value)
Remember that the slope of the linear equation is the same that the unit rate
Verify each case
1) we have
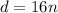
This is a proportional relationship between the variables d and n
The slope is
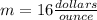
therefore
The unit rate is
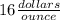
2) we have
First table
take two points from the table
(4,1) and (16,4)
substitute in the formula of slope
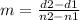
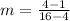
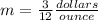
simplify
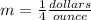
therefore
The unit rate is

3) we have

This is a proportional relationship between the variables d and n
isolate the variable d
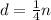
The slope is
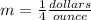
therefore
The unit rate is

4) we have
Second table
take two points from the table
(1,4) and (2,8)
substitute in the formula of slope
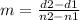
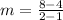
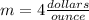
therefore
The unit rate is