To solve this problem, it is necessary to apply the concepts related to the Energy balance and the mass balance that allow us to find in each state the data necessary to find the total Power of the system through heat exchange.
From the tables of properties of the Water it is possible to obtain at the given pressures the values of the specific volume, the specific energy and the specific enthalpy.
Given these pressures then we have to
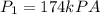

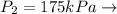 Saturated vapor
Saturated vapor
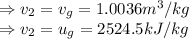
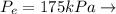 Saturated vapor
Saturated vapor
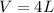
Considering the process performed, the kinetic and potential energy can be neglected as well as the work involved by specific interactions in the system. Although it is an unstable process it can be treated as a uniform flow process. Considering these expressions we can perform a mass balance for which
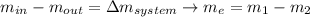
Similarly through the energy balance you can get that
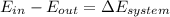
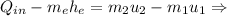 Since
Since
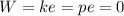
The initial mass, initial internal energy, and final mass in the tank are
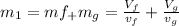
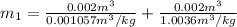

At the same time the internal energy can be defined from the mass in state 1 as,
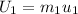
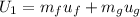
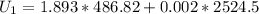
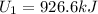
The calculation of mass in state 2 can be defined as
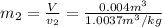
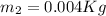
Then from the mass and energy balances,
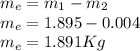
In this way the calculation of the heat of entry would be subject to
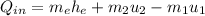


Therefore the Power would be given as
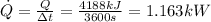
Therefore the highest rate of heat transfer allowed is 1.163kW