Answer:
P=1587.18 Pa
Step-by-step explanation:
Given that
V= 1.77 L =1.77 x 10⁻³ m³
m = 0.226 g
Vrms= 178 m/s
We know that ideal gas equation
P V = n R T
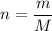
M=Molecular wight of the gas
P M = m R T -----------1
P=Pressure ,V=Volume ,n=Moles,R=Gas constant ,T=temperature
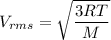 ------2
------2
From above two equation we can say that
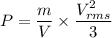
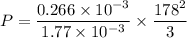
P=1587.18 Pa
The pressure of the gas is 1587.18 Pa