Answer:
8
Explanation:
we know that
If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube
Remember that all the spheres are similar
Let
z ----> the scale factor
V_1 ---> the volume of the large sphere
V_2 ---> the volume of the small sphere
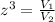
Find the scale factor
we know that
The radius of the large sphere is double the radius of the small sphere
so
The scale factor is 2
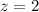
substitute the value oz z
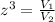
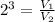
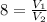
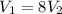
The volume of the large sphere is 8 times the volume of the small sphere