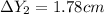Question

Using the result of the preceding problem, (a) calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen. (b) What would be the distance between fringes if the entire apparatus were submersed in water, whose index of refraction is 1.33?

Answer 1

To solve this problem it is necessary to apply the concepts related to the concept of superposition and the fringe separation for double slit experiment.

The equation can be written as

`\Delta y = (x\lambda)/(d)`

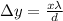
Where

`\Delta y` = Distance between fringes

x = distance between slits and screen

d = Distance between slits

`\lambda`= Wavelength

Our values are given as

d= 0.08mm

x =3m

`\lambda = 633nm`

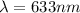
In this way replacing in the equation,

`\Delta y = (x\lambda)/(d)`

`\Delta y = (3m(633nm*((1*10^(-9))/(1nm))))/(0.08*((1*10^(-3)m)/(1mm)))`

`\Delta y = 2.37*10^(-2)m`

`\Delta y = 2.37cm`

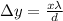
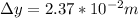
Therefore the distance between the fringes is 2.37cm

PART B) For the case in which it is submerged in water it is necessary to apply the relationship of the fringes with the index of refraction therefore

`\Delta Y_2 = (\Delta Y_1)/(n)`

`\Delta Y_2 = (2.37)/(1.33)`

`\Delta Y_2 = 1.78cm`