Question

The triceps muscle in the back of the upper arm is primarily used to extend the forearm. Suppose this muscle in a professional boxer exerts a force of 1.75 × 103 N with an effective perpendicular lever arm of 3.05 cm, producing an angular acceleration of the forearm of 115 rad/s2. What is the moment of inertia of the forearm, in kilogram meters squared?

Answer 1

To solve this problem it is necessary to apply the concepts related to Torque as a function of the Force and the distance radius where it is applied.

By definition the Torque can be expressed as

`\tau = F* r`

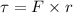
Where

F = Force exerted

r = Radius

Substituting we have to

`\tau = (1.75*10^3)(0.0305)`

`\tau = 53.375N\cdot m`

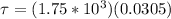
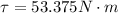
Through the second definition of the rotational Torque we can then find the moment of inertia for which we have to

`\tau = I\alpha`

Where

I = Moment of inertia

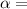`\alpha =` Angular acceleration

Replacing

`53.373 = I*115`

`I = 0.4641Kg \cdot m^2`

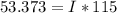
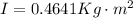
Therefore the moment of inertia is