Question

Use a finite sum to estimate the average value of f on the given interval by partitioning the interval into four subintervals of equal length and evaluating f at the subinterval midpoints.f(x)=x3 on [0, 2]

Answer 1

Average length of the given function

A(x)
`= (4)/(3)`

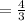
Explanation:

Step(i):-

Given function f(x) = x³ on [0,2]

Given interval by partitioning the interval into four subintervals of equal length

The average length of four subintervals of equal length

`Average length = (1)/(b-a) \int\limits^b_a {f(x)} \, dx`

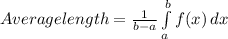
Step(ii):-

`Average length = (1)/(2-0) \int\limits^2_0 {x^3} \, dx`

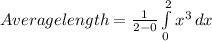
Now integrating

`\int\limits {x^(n) } \, dx = (x^(n+1) )/(n+1)`

`Average length = (1)/(2-0)( (x^3)/(3) )_(0) ^(2)`

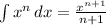
Final answer

Average length of the given function

`= (1)/(2-0)( (2^3)/(3) ) = (4)/(3)`