Question

Enter your answer in the provided box. An industrial chemist studying bleaching and sterilizing prepares a hypochlorite buffer using 0.450 M HClO and 0.450 M NaClO. (Ka for HClO = 2.9 × 10−8) Find the pH of 1.00 L of the solution after 0.040 mol of NaOH has been added.

Answer 1

`\large \boxed{7.62}`

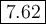
Step-by-step explanation:

1. pH of original buffer

(a) Calculate pKₐ

`\text{p}K_{\text{a}} = -\log \left (K_{\text{a}} \right ) =-\log(2.9 * 10^(-8)) = 7.54`

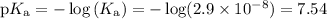
(b) Calculate the pH

We can use the Henderson-Hasselbalch equation to get the pH.

`\begin{array}{rcl}\text{pH} & = & \text{pK}_{\text{a}} + \log \left(\frac{[\text{A}^(-)]}{\text{[HA]}}\right )\\\\& = & 7.54 +\log \left((0.450)/(0.450)\right )\\\\& = & 7.54 + \log1.00 \\ & = & 7.54 + 0.00\\& = & 7.54\\\end{array}`

2. pH after adding strong base

(a) Find new composition of the buffer

The base reacts with the HA and forms A⁻

`\text{ Initial moles of HA} = \text{1.0 L} * \frac{\text{0.450 mol }}{\text{1.00 L}} = \text{0.450 mol = 450 mmol}\\\\\text{ Initial moles of A}^(-) = \text{1.0 L} * \frac{\text{0.450 mol }}{\text{1.00 L}} = \text{0.450 mol = 450 mmol}\\\\\text{Moles of OH$^(-)$ added} = \text{40 mmol}`

HA + OH⁻ ⟶ A⁻ + H₂O

I/mmol: 450 40 450

C/mmol: -40 -40 40

E/mmol: 410 0 490

(b) Find the new pH

`\begin{array}{rcl}\text{pH} & = & \text{pK}_{\text{a}} + \log \left(\frac{[\text{A}^(-)]}{\text{[HA]}}\right )\\\\& = & 7.54 +\log \left((490)/(410)\right )\\\\& = & 7.54 + \log1.195 \\& = & 7.54 +0.0774\\& = & \mathbf{7.62}\\\end{array}\\\text{The new pH is $\large \boxed{\textbf{7.62}}$}`