Question

The half life of a certain substance is about 4 hours. The graph shows the decay of a 50 gram sample of the substance that is measured every hour for 9 hours.

A graph shows time (hours) labeled 1 to 10 on the horizontal axis and quantity (grams) on the vertical axis. A line decreases from 0 to 9.

Which function can be used to determine the approximate number of grams of the sample remaining after t hours?

y = 25(0.15)t
y = 25(0.85)t
y = 50(0.15)t
y = 50(0.85)t

Answer 1

D

Explanation:

50(.85)^t

Answer 2

`y = 50(0.85)^(t)`

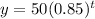
Explanation:

Let the equation that models the decay of the substance is given by

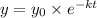`y = y_(0) * e^(-kt)` ........... (1)

where y is the amount of the substance remaining after t hours and
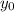`y_(0)` represents the initial amount of the substance and k is the decay rate constant.

Now, given that the half-life period of the substance is 4 hours.

So, from equation (1) we can write

`0.5 = e^(- 4k)`

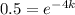
Now, taking ln on both sides we get

ln 0.5 = -4k

⇒ k = 0.17328

Therefore, the equation (1) becomes

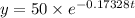`y =50* e^(-0.17328t)` {Since the initial amount of the substance was 50 gm}

⇒
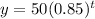`y = 50(0.85)^(t)` (Approximate) (Answer)