Question

J&J Manufacturing issued a bond with a $1,000 par value. The bond has a coupon rate of 7% and makes payments semiannually. If the bond has 20 years remaining and the annual market interest rate is 9.4%, what will the bond sell for today?

a. $761b. $787c. $746d. $785e. $796

Answer 1

The correct option is d. $ 785

Explanation:

Since,

`\text{Bond price}=(C)/(YTM)(1-(1)/((1+(YTM)/(2))^(2M)))+(FV)/((1+(YTM)/(2))^(2M))`

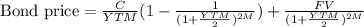
Where,

C = Annual coupon payment,

FV = Face value,

M = Maturity in years,

YTM = yield to maturity,

Here,

FV = $ 1,000,

C = 7% of 1000 =
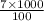`(7* 1000)/(100)` = 70,

M = 20 years,

YTM = 9.4% = 0.094,

By substituting the values,

`\text{Bond price}=(70)/(0.094)(1-(1)/((1+(0.094)/(2))^(40)))+(1000)/((1+(0.094)/(2))^(40))`

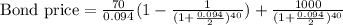
= $ 785.3454 ( Using calculator )

≈ $ 785

Hence, OPTION d. is correct.