Answer:
12.65m³/ sec
Step-by-step explanation:
The process flow shown in the attachment along with this explanation, with point 2 taken in the liquid at the entrance to the nozzle and point 3 at the exit of the nozzle.
Since A₁ is very large compared to A₂, v₁ ≅ 0. The pressure p₂ is greater tha₁n 1atm (101.3kN/m3) by the head of fluid of Hm. The pressure p₃ which is at point 3 is at 1atm. Using point 2 as a datum, z₂=0 and z₃=0. From bernoulli’s equation
z₂g+ v₂²/2 + p₂/ρ = z₃g+ v₃²/2 + p₃/ρ
we can rearrange the above Bernoulli’s equation as
z₂g+ v₂²/2 + p₂-p₃/ρ = z₃g+ v₃²/2
0+0+p₂-p₃/ρ = 0 + v₃²/2
Solving for v₂
v₃ ⇒
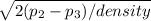 ..........Equation 1
..........Equation 1
since p₂-p₁ = Hρg and p₁ = p₃ ( both at 1atm)
H = p₂-p₃/ρg
p₂-p₃ = Hρg...............................Equation 2
put Equation 2 into Equation 1
v₃ =
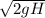 .....................Equation 3
.....................Equation 3
v₃ =
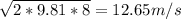
The volumetric flowrate in 1.00sec is given as
flow rate = v₃A₃= 12.65×

=0.202m³/sec