Question

A 16.6 kg object on a horizontal frictionless surface is attached to a spring with k = 2470 N/m. The object is displaced from equilibrium 28.1 cm horizontally and given an initial velocity of 12.6 m/s back toward the equilibrium position. What are (a) the motion's frequency, (b) the initial potential energy of the block-spring system, (c) the initial kinetic energy, and (d) the motion's amplitude?

Answer 1

To solve this problem it is necessary to apply the concepts related to Period in a spring, elastic potential energy and energy in simple harmonic movement.

From the definition we know that the period can be expressed as

`T = 2\pi \sqrt{(m)/(k)}`

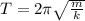
Where

m= Mass

k = Spring constant

Our values are given as

m = 16.6Kg

K = 2470N/m

Therefore the period would be

`T = 2\pi \sqrt{(m)/(k)}`

`T = 2\pi \sqrt{(16.6)/(2470)}`

`T = 0.515s`

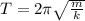
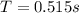
PART A) The frequency is the inverse of the period therefore

`f = (1)/(T)\\f = (1)/(0.515)\\f = 1.9417Hz`

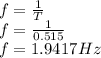
PART B) Elastic potential energy depends on compression and elasticity therefore

`PE = (1)/(2)kx^2`

`PE = (1)/(2) (2470)(0.281)^2`

`PE = 97.51J`

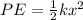
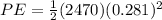
PART C) Kinetic energy depends on mass and speed therefore

`KE = (1)/(2)mv^2\\KE = (1)/(2) (16.6)(12.6)^2\\KE = 1371.7J`

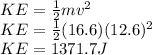
PART D) As energy is conserved, the total energy is equivalent to the dual ratio of the elasticity constant and the amplitude, mathematically,

`KE+PE = (1)/(2)kA^2`

`1371.7+97.51 = (1)/(2)2470A^2`

`A = \sqrt{(1415*2)/(2470)}`

`A = 1.07m`

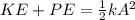
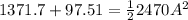
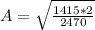
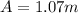
Therefore the motion's amplitude is 1.07m