Question

A ray of light reflects off of 2 mirrors that are perpendicular to each other. It hits the first mirror at an angle of 30° from perpendicular, 10 cm from the corner, calculate angle between the incoming and outgoing light.

Answer 1

Answer:
`180^(\circ)`

Step-by-step explanation:

we know that angle of incidence from vertical is equal to angle of reflection from mirror.

incoming ray angle
`\theta =30^(\circ)`

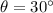
Reflected ray angle
`\theta =30^(\circ)`

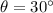
Now this ray will incident on another mirror with angle of incidence
`=60^(\circ)`

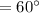
reflected ray angle
`=60^(\circ)`

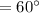
now the outgoing ray is parallel to incoming rays

angle between them is
`180^(\circ)`