Question

A blue car with mass mc = 459.0 kg is moving east with a speed of vc = 19.0 m/s and collides with a purple truck with mass mt = 1245.0 kg that is moving south with a speed of vt = 10.0 m/s . The two collide and lock together after the collision. 1) What is the magnitude of the initial momentum of the car? 2) What is the magnitude of the initial momentum of the truck? 3) What is the angle that the car-truck combination travel after the collision? (give your answer as an angle South of East) 4) What is the magnitude of the momentum of the car-truck combination immediately after the collision? 5) What is the speed of the car-truck combination immediately after the collision? 6) Compare the initial and final kinetic energy of the total system before and after the collision:

Answer 1

1)
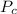`P_c` = 8721 Kg*m/s

2)
`P_t` = 12450 Kg*m/s

3) θ = 55.03°

4) P = 15182 Kg*m/s

5) V = 8.91 m/s

6)
`E_i>E_f`

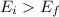
145099.5 J > 67638 J

Step-by-step explanation:

1) The momentum is calculated by the next equation:

P = MV

where M is the mass and V is the velocity

so, the linear momentum of the car is:

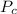`P_c` = (459)(19)

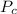`P_c` = 8721 Kg*m/s

2) the linear momentum of the truck is:

`P_t` = (1245)(10)

`P_t` = 12450 Kg*m/s

3) For answer this we will use the law of the conservation of the linear momentum where:

`P_i = P_f`:

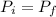So, we will do this for each axis:

First on axis x:

`M_cV_c = V_(sx)M_s`

Where
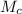`M_c` is the mass of the blue car,
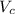`V_c` is the velocity of the car,
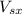`V_(sx)` is the velocity of the system in x after the collition and
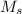`M_s` is the mass of both cars. Replacing, we get:

`(459)(19) = V_(sx)(1245+459)`

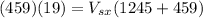
Solving for
`V_(sx)`:

`V_(sx) = 5.11 m/s`

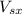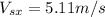
Second, on axis y:

`M_tV_t = V_(sy)M_s`

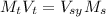
Where
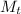`M_t` is the mass of the truck,
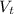`V_t` is the velocity of the truck,
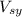`V_(sy)` is the velocity of the system in y after the collition and
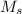`M_s` is the mass of both cars.

`(1245)(10) = V_(sy)(1245+459)`

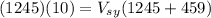
Solving for
`V_(sy)`:

`V_(sy) = 7.306 m/s`

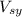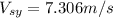
Now using the definition of tangent:

θ =
`tan^(-1)((7.306)/(5.11))`

θ = 55.03°

4) First, we have to find the magnitude of the velocity using the pythagorean theorem as:

V =
`√(7.306^2+5.11^2)`

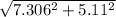
V = 8.91 m/s

With the velocity, we find the momentum as:

P = MV

P =(1245+459)(8.91)

P = 15182 Kg*m/s

5) This was calculated before, so:

V = 8.91 m/s

6) The energy of the total system before the collision is calculated as:

`E_i = (1)/(2)M_cV_c+(1)/(2)M_tV_t`

`E_i = (1)/(2)(459)(19)^2+(1)/(2)(1245)(10)^2`

`E_i = 145099.5 J`

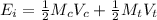
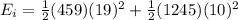
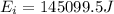
The energy of the total system after the collision is calculated as:

`E_f = (1)/(2)M_sV^2`

`E_f = (1)/(2)(1245+459)(8.91)^2`

`E_f = 67638 J`

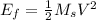
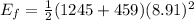
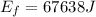
So, the energy of the system before the collision is bigger than the energy of the system after the collision.