To solve this problem it is necessary to apply the concepts related to the Stefan-Boltzman law that is responsible for calculating radioactive energy.
Mathematically this expression can be given as
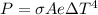
Where
A = Surface area of the Object
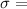 Stefan-Boltzmann constant
Stefan-Boltzmann constant
e = Emissivity
T = Temperature (Kelvin)
Our values are given as
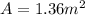

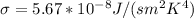
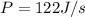
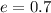
Replacing at our equation and solving to find the temperature 1 we have,
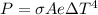

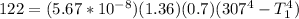
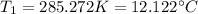
Therefore the the temperature of the coldest room in which this person could stand and not experience a drop in body temperature is 12°C