Question

In an experiment to measure the speed of light using the apparatus of Armand H. L. Fizeau (see Fig. 34.2), the distance between light source and mirror was 11.45 km and the wheel had 720 notches. The experimentally determined value of c was 2.998 3 108 m/s when the outgoing light passed through one notch and then returned through the next notch. Calculate the minimum angular speed of the wheel for this experiment.

Answer 1

First of all although there is no image described at the bottom, attached that fits perfectly with the experiment carried out.

From this perspective to solve this problem we must be guided by the kinematic equations of angular motion.

By definition we know that through the number of Notches it is possible to identify the total angular displacement in revolutions, that is to say

`\Delta \theta = (1)/(720) rev`

`\Delta \theta = (2\pi)/(720)rad`

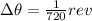
The kinematic equations of motion tell us that speed (in this case that of light) can be expressed as

`c = (d)/(t)`

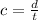
Where

d = distance

t = Time

Since the light has a round trip we have to

`c = (2d)/(\Delta t)`

`\Delta t = (2d)/(c)`

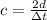
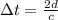
Our values are given as

`d = 11.45km = 11.45*10^3m`

`c = 2.9983*10^8`

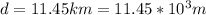
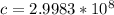
From these same equations we have then that

`\omega = (\Delta \theta)/(\Delta t)`

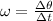
Replacing with the two previous values found

`\omega = ((2\pi)/(720))/(2d/c)`

`\omega = ((2\pi)/(720)*(2.9983*10^8))/(2(11.45*10^3))`
`\omega = 114.304rad/s`

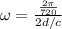
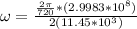
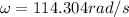
Therefore the minimum angular speed of the wheel for this experiment is 114.304rad/s