Answer:
Speed of the jet is 100 m/s.
Step-by-step explanation:
Given that,
Mass of the jet, m = 10 kg
Spring constant, K = 160 N/m
Distance covered by the aircraft to stop, x = 25 m
Let v is the landing speed of the plane. It can be calculated using the conservation of mechanical energy. Since, the kinetic energy of the plane must be equal to the elastic potential energy of the spring as :
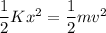
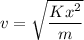
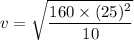
v = 100 m/s
So, the speed of the jet when it first hooks on to the cable is 100 m/s. Hence, this is the required solution.